今回の記事では、経済学・経済政策で学習する「消費者行動と需要曲線」についてご紹介していきます。
現代社会における経済活動の中では、誰もが一消費者であります。
その消費者の行動原理は理論体系化されており、この単元ではその理論を学習するとお考えください。
効用、選好、無差別曲線、予算制約線etc.何やら難解なワードが出てはきますが、つまるところ一消費者であるあなたの心理を説明したものです。
日常のショッピングにおける、あなた自身の感情と照らし合わせて考えて頂ければ、当然のことを確認していることに気付かれるのではないでしょうか。
それでは、さっそく消費者行動について確認していきましょう!
目次
消費者行動を決定する効用と選好ってどんなもの?

まずは、効用と選好の意味を確認していきます。
効用というのは、財を消費することで得られる満足感のことをいいます。
コーヒーが好きなAさんとお茶が好きなBさんが存在した場合、Aさんはお茶を消費するよりもコーヒーを消費する方が効用が高まるはずですし、Bさんはお茶を消費したケースで効用が高くなります。
また、選好というのは好みのことです。上記のケースでいうと、Aさんはコーヒーを選好しますし、Bさんはお茶を選好します。
つまり、AさんとBさんは異なった選好を持つといえます。
【効用を可視化①】効用関数を理解しよう!
では、効用をもう少し掘り下げて考えていきます。
お酒が好きなAさんは、ビールとウイスキーを好んで飲むと仮定します。
そんなAさんのビールとウイスキーの消費量、またそれぞれのパターンから得られる効用をまとめたものが図1の表です。
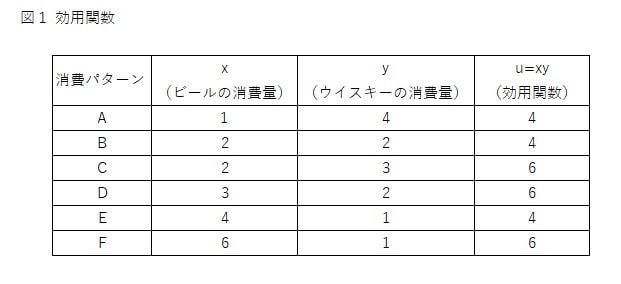
効用uはそれぞれの消費量を乗じて算出します。つまり、u=xyで表され、この数式が効用関数です。
なお、Aさんはこの表にある消費量以上のお酒は呑めないものと考えてください。
お酒を呑めば呑むほど満足感が無限に高まっていく人はいませんからね、恐らく(笑)
パターンAとBを比較すると効用はどちらも4となり、どちらも同程度の満足感が得られると解釈します。
またパターンAとCとの比較では、Cの方がより高い満足感をもたらしてくれると解釈します。
つまりAよりもCという消費パターンを選択することが効用を最大化するという意味では望ましいといえるわけです。
【効用を可視化②】無差別曲線を理解しよう
お次に、効用関数を図示化してみていきましょう。
同水準の効用を得られるようなビールとウイスキーの消費量の組み合わせをプロットしたものが、以下の図2の無差別曲線となります。
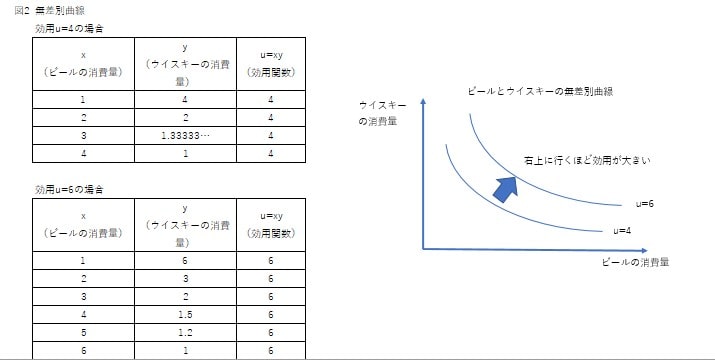
縦軸にウイスキーの消費量、横軸にビールの消費量を設定し、効用が4となるケース、6となるケースをそれぞれプロットすると、左下に凸となる曲線が出来上がります。
効用は大きい方が望ましいですから、この曲線が右上にあるほど満足度が高い状態にあるといえます。
つまり、満足度を上昇させるためには無差別曲線自体を右上にシフトさせる必要があります。
一方、同一曲線上にある消費量については、どの位置であっても満足度は変わらないことを示しています。
消費パターンの組み合わせを変化させても、同一曲線上にある限り効用は一定ですので、満足度も一定と考えるのです。
ビールの価値が減少する?限界代替率逓減ってどういうこと?

さらに、先ほどの図2の表に示された効用u=6のケースを用いて、ビールとウイスキー、それぞれ1杯あたりの価値の変化について確認していきます。
ビールを1杯から2杯に増やすとき、ウイスキーを6杯から3杯に減少させても、効用6を維持できていることが確認できるかと思います。
ビール1杯とウイスキー3杯の価値が同程度といえるわけです。
では、ビールを5杯から6杯に増やすときはどうでしょうか?
ウイスキーは1.2杯から1杯までしか減らすことができなくなっています。
つまり、ビール1杯はウイスキー0.2杯と同程度の価値となっています。
このように2つの消費財の組み合わせにおいて、片方の消費量(このケースではビール)が増えれば増えるほど、他方(このケースではウイスキー)の価値が増加することが確認できます。
言い換えるとビールの消費量が増えるほど、ビールの価値が低下していることを意味しています。
このような現象を限界代替率逓減といいます。
一方の消費量が増加すればするほど、そこから得られる効用は減少するのです。
予算の制約を可視化しよう!予算制約線とはどんなもの?
ここまでに消費者の効用を確認してきました。
無差別曲線を右上にシフトさせればさせるほど幸福になれるわけです。
しかし、一般的な経済活動においては、無差別曲線を無尽蔵に右上にシフトさせることなどできません。
お小遣い、つまり予算の制約があるからです(笑)
ここでは、ビール1杯500円、ウイスキー1杯250円、本日の予算は2,000円と仮定します。
これを数式に当てはめると「500x × 250y ≦ 2,000」となります。
数式を展開すると、「y ≦ -2x + 8」となり、それを図示化したものが以下図3の予算制約線です。

当然のことながら、予算の範囲内で消費できる量というのは予算制約線の内側に限られることになりますから、消費者はこの制約の中で効用を最大化することになります。
無差別曲線と予算制約線により、効用の最大化を図る!
ここまで確認してきた無差別曲線と予算制約線を組み合わせて考えることで、その予算の範囲内における効用最大化を図ることができます。
以下の図4は予算制約線と3つの無差別曲線を描いたものです。
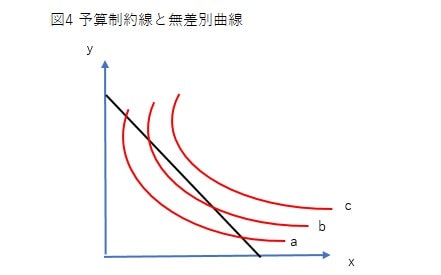
この3つの無差別曲線の中で、現実的な効用最大化をもたらしてくれるのはどれでしょうか?
無差別曲線は右上にシフトするほど効用が大きいわけですから、最も効用を最大化してくれるのはcの無差別曲線となります。
しかし、予算制約線を確認してみるとcは予算を超えた位置にあることがわかりますので、cはそもそも選択することができません。
予算制約線の内側を通過しているのはaの無差別曲線です。
予算面での制約はクリアしていることがわかりますが、予算制約線と2点で交わっています。
これは予算制約線の下側を通過していることとなり、予算をもっと有効に活用する余地を残しているといえます。
よって、aはまだまだ効用を伸ばす余地があると考えられますので、効用最大化を実現できているとはいえません。
最後にbの無差別曲線ですが、こちらは予算制約線と一点で交わっていることが確認できます。
予算制約範囲の上限で効用を得ていることになりますので、効用を最大化している消費の組み合わせはbの組み合わせであることがわかります。
このように、予算制約線と無差別曲線が一点で交わっている状態が効用を最大化できている状態となります。
価格が下がればもっと買いたい!需要曲線を確認しよう
さて、ここまでは個人が2財を組み合わせて消費するケースでの効用を学習してきました。
では一つの消費財に着目したケースでは、どのようなことがいえるのでしょうか。
その考え方を図示化したものが、図5の需要曲線となります。
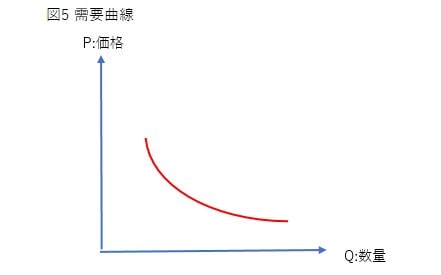
こちらの需要曲線では、縦軸に価格(Price)、横軸に数量(Quantity)をとっており、ある一財の需要曲線は右下がりの曲線を描きます。
これは、価格が下がれば社会全体の需要量が増加するということを意味します。
価格が下がれば消費する人が増えますし、各々の消費量が増えることも想定されます。
そんな当たり前のことを示しているのが需要曲線の右下がり形状なのです。
ここについては、企業サイドの供給曲線との均衡点を探ることになりますが、ここではひとまず需要の基本原則ともいえる「価格が下がれば需要が増える」ということをしっかりと頭の中に叩き込んでおきましょう。
まとめ

今回は、経済学・経済政策の消費者行動と需要曲線を確認してまいりました。
冒頭でも述べましたが、難解なワードが出てはきますが、結局のところ消費者の感情というのは我々の中に根付いているものばかりです。
たくさん消費すればするほど満足度は低下しますし、価格が下がれば社会的な需要量は増加します。
そういった意味では、腑に落ちやすい内容ばかりかと思います。
自身の感覚と経済学の理論を結び付けて考えることで、理解は促進されるはずです。
効率的に学習を進めて、中小企業診断士試験を攻略していきましょう!